Investors often say that standard deviation is a bad way to measure investment risk because it penalizes upside volatility as well as downside. I agree that standard deviation isn’t a great measure of risk, but that’s not the reason. A good risk measure should penalize upside volatility, because upside volatility is bad.

A sure-thing return is better than a volatile return, even if the volatile return is guaranteed to be positive.

I will first explain my reasoning without using too much math, and then provide a more rigorous explanation using math in the next section.

As an illustration, suppose there’s some investment that only ever produces positive returns, and the distribution of outcomes looks like this:

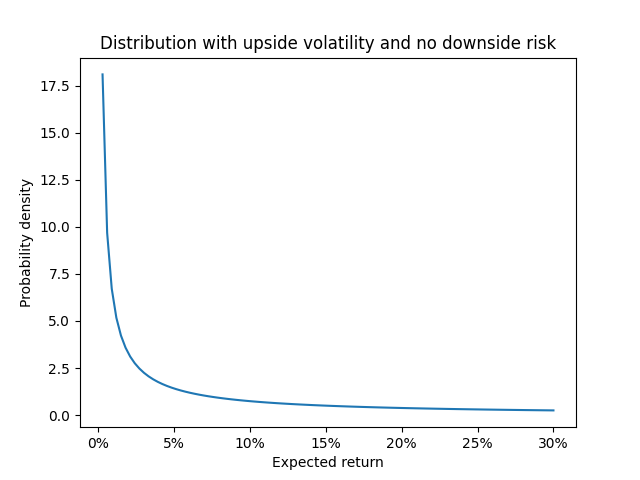
(For those who want to know, that’s a gamma distribution with shape 0.1 and scale 2.)

This investment has plenty of upside volatility, but no downside volatility—it can never earn a negative return.

The investment has an expected return of 5%. But if you buy it, most of the time you will earn less than 5%. If you’re investing to prepare for your future, which would you rather have: a guaranteed 5% return? Or a volatile return with an average of 5%, but where you probably end up getting less than that?

With the guaranteed return, you’re guaranteed to be set for retirement as long as you put enough money into savings. With the volatile investment, even though you know you won’t lose money, you’re still not sure how much you’ll end up with.

Mathy explanation

Suppose Alice is an investor with logarithmic utility of money, which is a classic risk-averse utility function. I generated one million sample outcomes using our upside-volatile distribution and found that Alice’s expected utility was 0.12. (0.12 of what? 0.12 utility. It doesn’t mean anything concrete; it’s just a number.)

Alice has the opportunity to buy a safe investment with the same expected return, but zero volatility. The guaranteed investment has 0.18 utility for Alice—considerably higher than the volatile investment, even though she has no risk of losing money.

Bob is twice as risk-averse as Alice.¹ His utility for the guaranteed investment is 0.17, and his expected utility for volatile asset is 0.09. Like Alice, he prefers the sure thing. For him, the sure thing is nearly twice as good.

I believe Bob’s utility function is more representative of a normal person’s. So for a normal person, the sure thing is much better than the volatile investment, even though the volatility is all upside.

Skewness still matters

I’m not saying standard deviation is a perfect measure of risk, because it’s definitely not.

Imagine you have a choice between two investments that have expected returns distributed like this:

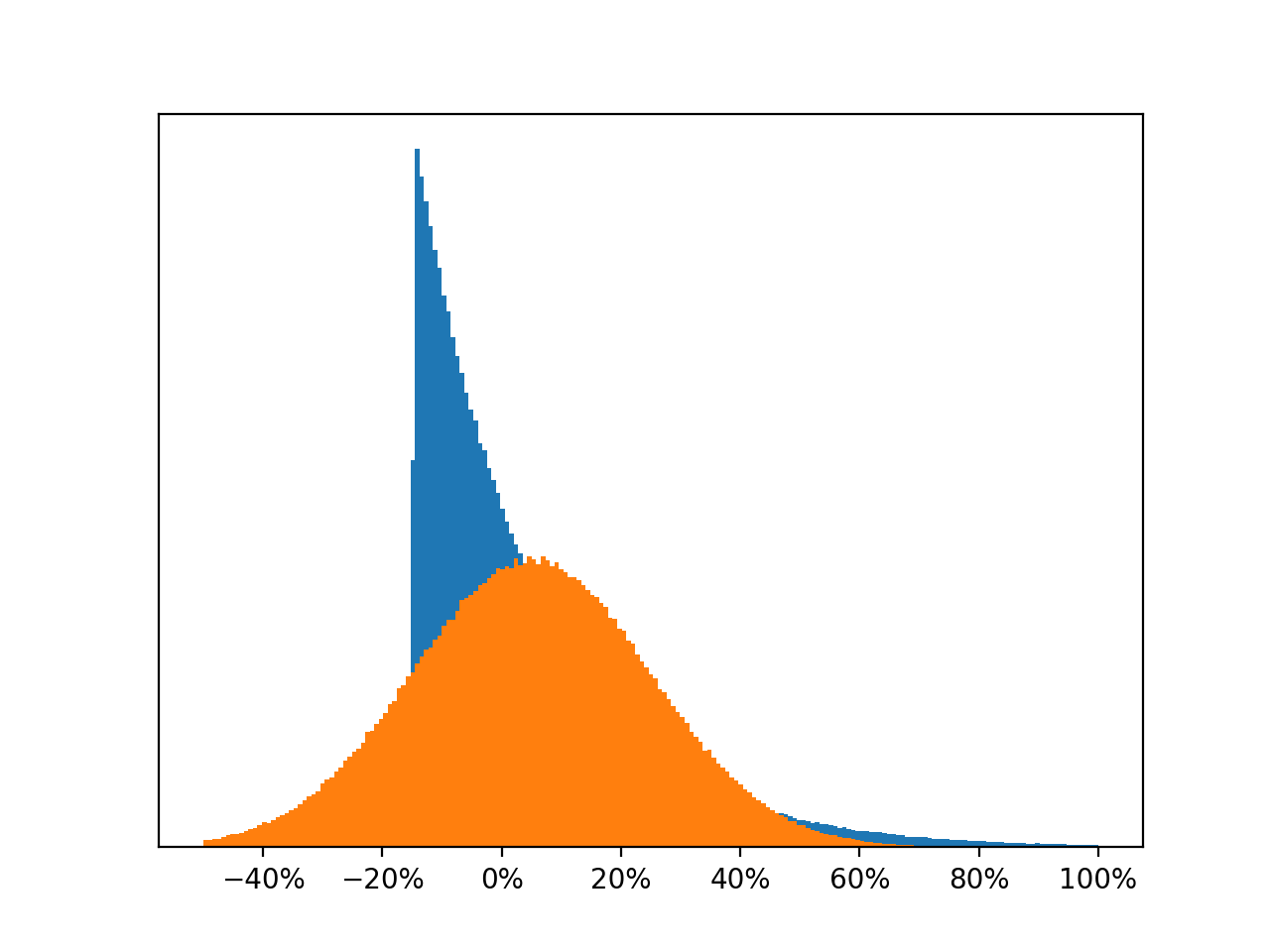
These distributions have the same standard deviation. But the blue distribution is still preferable to the orange one, because the orange one has a much bigger risk of losing money. It’s symmetric, whereas the blue distribution is right-skewed. Just looking at standard deviation doesn’t capture that.

Or compare these two distributions:

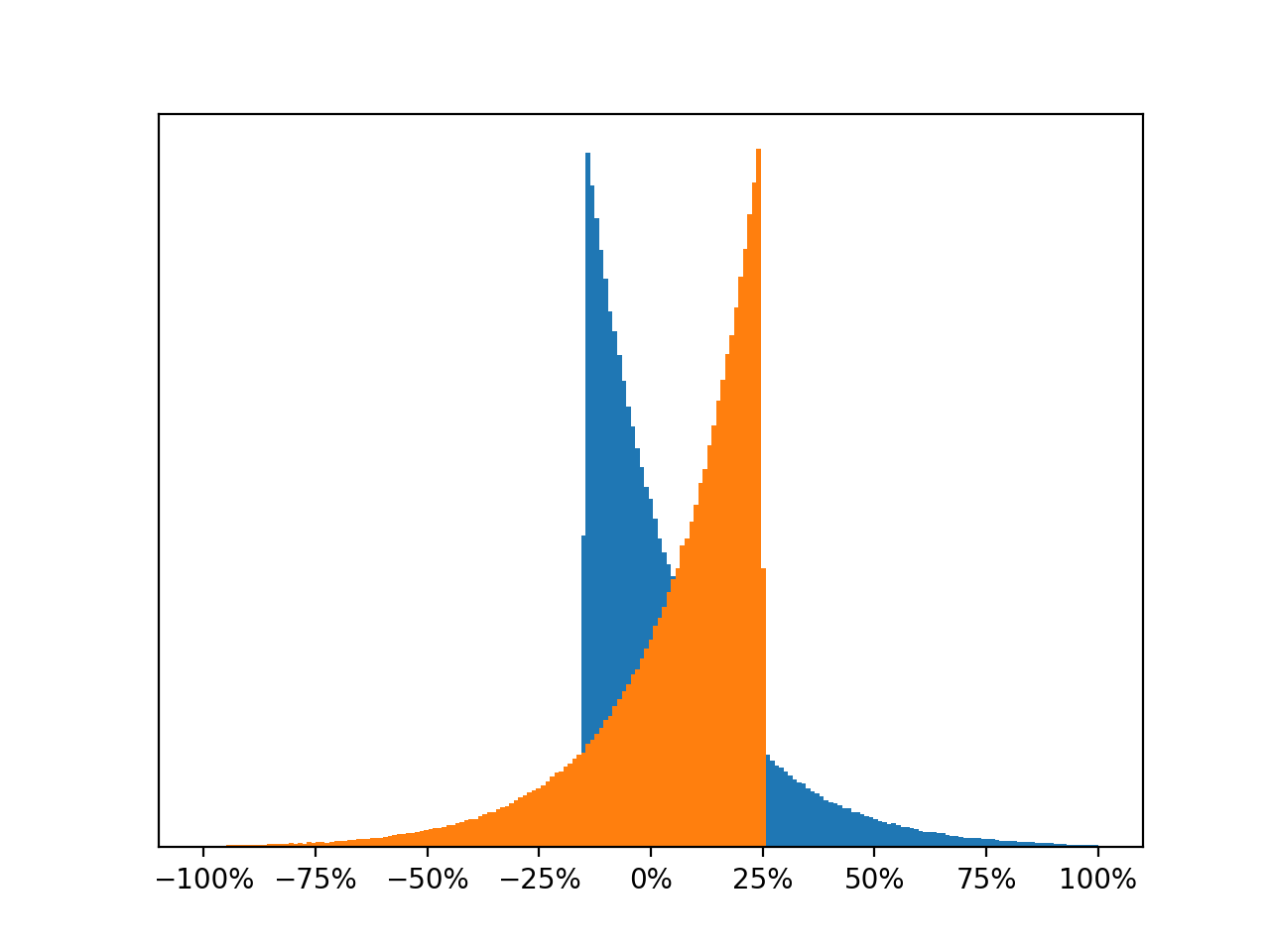
Both distributions have the same mean and standard deviation, but the orange one looks horrible. I would definitely not want to invest in the orange one. The left-skewed distribution looks much less appealing than the right-skewed one.

Yes, upside volatility is bad, but downside volatility is worse. A guaranteed constant return is better than an always-positive but uncertain return, which in turn is better than an uncertain return that might be negative. (Assuming, of course, that all three have the same expected return.)

Posted on Nov 09, 2025

Notes